This post was updated for 808 day 2022. Some errors and unclear explanations were fixed.

This post first appeard on the SS-30M blog on 02/11/21

808 Snare Continued...

I have been happily using my Mutant Snare since the investigation into 808 snare tuning last year, but I still have an itch to create a solution for tuning the 808 snare in a more flexible way.

The conclusion is that I now have design parameters for my own tuneable 808 snare and as a bonus I figured the vexed problem of Q and the decay time!

Mut' Point

After considering my options I decided that modding the Mutant Snare was not the way to go. There will be no Mutoid Snare. Instead it will have to be a whole new module to get what I want.

However, I have made a list of mods that would not be particularly invasive and would make the Mutant Snare even more flexible. The main idea is to bring the filter CV jumper to a switch. This jumper setting selects between the snappy envelope and osc 1 as the source of CV for the filter cut-off when there is no CV external input. Anyway, that's a whole other project, but a (yep) side (drum, geddit?) panel would be cool.

The 80'81 SD

What I really want is an 808 snare with full control over both the oscillators. In fact, I wanted not only independent pitch controls, and therefore a tuneable ratio between for the combined shell tone, but also a switch selecting between the original 1980-81 tuning and the 1981-82 revision.

The two new controls on the 808 snare are:

A switch to select between the two values of capacitor in the T-resonator circuit.
Variable resistors for 'R2' of the bridged-T network - i.e. R197 and R198.

These new features are in addition to the usual Tone control, to balance the mix of the two oscillators and Snappy, to balance the amount of white noise 'snare' sound to the oscillators snare.

Other features are considered below, but the initial concept is to keep the design simple and only add the tuning controls, which I feel are "missing".

Switch Cap

Recall that the June 1981 TR-808 service manual describes a change to one capacitor in each of the two bridged-T network oscillators in the snare circuit. This change lowers the pitch of the 'shell' part of the snare drum and also subtly alters the ratio of their tuning.

This new switch is needed to achieve the full range, because varying a resistor in the bridged T-network alone would not achieve the same result. Ideally, when the tuning controls are in a central position (more on that later) the behaviour ought to be switching the overall tuning from original (1980-81) to new (1981-82).

Another consideration here is the Q factor of the bridged T. Whilst adjusting the resistance in the circuit can tune over a wide range the Q will change too, and not in the same way as switching the capacitor. This means that the decay time would change too. More on that below too.

A switch for the two capacitor values is thus required to maintain a 'true' 808 sound and can be used without touching the tuning controls to quickly select either the original or revised design.

Tuning Fine

Whilst the capacitor switching is a coarse control over the tuning there is also a desire on my part to be able to fine tune both oscillators. As noted above, this would correct for what I feel is lacking in the Mutant Snare. The need for this was covered in the previous post, but to be clear the benefits are:

General facility to achieve different sounds, beyond standard 808s, above and below the nominal
Adjustment of ratio, so that the tones are either in or out of harmony as required
Adjustment of tuning to achieve specific tunings or any arbitrary non-standard tuning found on real machines, either circa 1980-82 or now on aged machines.

That last one, in the extreme, would make it possible to dial-in any particular machine's tuning. Want that classic Def Jam/Beastie Boys snare? Just get the tuner out and go for it! Or how about the latest clone, or Roland digital version? All possible.

Resistor Choices - Or, R2 Indeed To?

The most obvious solution for tuning is to replace the single fixed values for R197 and R192 with a fixed resistor (a) of half the value and a linear variable resistor (b) of the same value in series. This is the suggested modification for the TR-606 snare tuning mentioned in the previous post.

In this configuration, the mid-point of the variable resistor results in the same impedance as the original single fixed value and the extremes of the range are plus and minus half that resistance.

R197 is 820k and R198 is 1M and the ideal variable and fixed resistors would thus be as follows:

R197a 410K & R197b 820K
198a 500K & R198b 1M

As 820K pots are not commonly available this means I need to decide what to use instead.

This brings into question the range of tuning and what I actually want or need, so before assuming the values given above, what is the range supposed to be?

R2 Detune or R1?

Before that though, what about R1? I am reminded that for the AteOhAte Toms project I struggled to find the required 500R potentiometers in the size I wanted. This made a complicated mechanical design even more fiendish as I could only source right-angled mounting 500R pots in the right size.

What size would I need for R195 and R196 though? They are 680R and 2K2 respectively, so 1K would seem right for R196, but R195 is more difficult. Perhaps that could be changed by tweaking R197? Hmm! But do I prefer this resistor being variable, or R2? Which is best? Why did Roland make R1 variable for the Conga/Toms?

The maths is the only way to know for sure. What I found is that the tuning and Q range are much wider when reducing R1 by half the value. For example, using R195 +/- 320R, it would be -20Hz and +96Hz Q is similarly lopsided. I had a similar problem altering R2, but by much smaller proportions, as we'll see.

So, why did Roland choose that variation for their Conga/Toms? Note that:-

they all use the same R1/R2 values and simply alter the C1/C2 for each of low, mid, hi drums.
R2 is 820K is each case, which is the same as the low shell of the snare,
the 1K + 500 pot pair are in the same ball-park as R195 at 680R.

A-ha, though! The fixed resistor is twice the value of the pot, not half, so the range of R1 is 1K - 1.5K. This is a range of +/-0.25, not +/- 0.5. If I recalculate for a 680R this would be 510-680-850 a range of just 340R on the pot with a 510R in series.

In any case this this too small a value and not working out. Back to R2.

Tone Ranger

Let's look at the range of values I measured for real 808s and their clones etc. (all values in Hz)

Original values: Low = 202 - 254 / High = 443 - 499

Revised Values: Low = 159 - 189 / High = 326 - 374

Now let's look at the size of the range:

Original values: Low = 52 / High = 56

Revised values: Low = 40 / High = 48

Allowing for the unscientifically small sample involved, I think it's fair to say that at tuning range of around 50Hz, or slightly higher would be suitable to obtain all of the various types I found in the wild.

It's now worth pointing out that for the examples I found with original tuning were generally lower pitched than the calculated value and the examples with revised values were more evenly spread above and below the nominal. Whether this is significant I can't say, but the correct degree of the tuning range remains open to debate.

Home (In) On the Range

The ideal potentiometer for the R197 of 820K is not available, so let's try 1M. The required mid-point is the same as R197 - 820K so let's see what that looks like:

i.e. let the range of frequency be around +/- 50Hz with variable resistor values +/- 500K (1M pot):

320K = 400Hz
820K = 250Hz
1.32M = 198Hz

This is is now a wider range than we wanted to begin with, so let's try a 500K resistor instead and see how narrow that is

i.e. let the range of frequencies be around +/- 50Hz with values of variable resistor +/- 250K (500K pot):

570K = 300Hz
820K = 250Hz
1.07M = 219Hz

The range is now below what we wanted at 80Hz and the lower limit of the range is a bit too high. However, this is probably as good as it's going to get. The required centre frequency is in the middle of the potentiometer and trying to shift the range to be more central (+/-40Hz) is possible, but at the expense of that centring.

Out Of Bounds

There's another issue to look at with narrowing the range. When I flip the switch to the revised capacitor values.

i.e. let the range of frequencies be around +/- 50Hz with values of variable resistor +/- 250K (500K pot) and revised cap of 56nF:

570K = 208Hz
820K = 175Hz
1.07M = 152Hz

As you can see, by comparing with the calculation above, this range leaves a gap between the original and revised range of values. You can't bridge it with the potentiometer values. However, I note that this holds true for the actual 808s out there too. You can't find 808s that sit in the middle of the range.

This raises another question: what if there where a third capacitor value between the original and revised? This would be either 39nF as the nearest to halfway between 27nF and 56nF (41.5).

i.e. let the range of frequencies be around +/- 50Hz with values of variable resistor +/- 250K (500K pot) and revised cap of 39nF:

570K = 249Hz
820K = 208Hz
1.07M = 182Hz

I mean, why not? This third band allows for a full range, from end-to-end. Assuming I can find a DP3T switch which I like there's not much wrong with the idea and it adds that little bit more versatility. It will make tuning in some values easier anyway.

It also begs the question, why did Roland shift so far off the original tuning? It's not a subtle adjustment they made. They admit to rushing the snare after spending so long on the kick, but as we can't currently know that, all I can say is let's take that middle ground they left and see what's there.

High Note

That just leaves the high oscillator, which has an R2 value or 1M. I'll cut to the chase and tell you that 1M is too large a range, so I also went with 500K, as with the low oscillator.

i.e. let the range of frequencies be around +/- 50Hz with values of variable resistor +/- 250K (500K pot) and original cap of 6.8nF:

750K = 576Hz
1M = 499Hz
1.25M = 446Hz

That's a range of 130Hz. Not bad. Next?

Tabul-8

We now have a tuning control and 3-way switch for each of the two oscillators giving... oooh, all sorts of values. Let's take a look (you might need to scroll over a bit).

Oscillator	Band	Frequency (Hz)
High(Right)	Original (6.8nF)							446	499	576
	Centre (10nF)						368	411	475
	Revised (15nF)					300	336	388
Low(Left)	Original (27nF)			219	250	299
	Centre (39nF)		182	208	249
	Revised (56nF)	152	173	208

Cue the Q

It's not quite the end of the story though. We should really look at Q. Even though I didn't manage to work out how the Q factor is mathematically related to the decay time of the oscillators in the previous post it's clear that if Q changes a lot then there will be a problem. I don't want very long or very short sounds so let's see what the tuning does to Q.

It's actually a bit interesting! When I calculate the Q for the original, revised and centre bands across the range of the tuning each result is different. But, when I see what percentage the Q changes by, across the range it's the same. Exactly the same, to at least four decimal places. That seems wrong. Almost.

In each band the resistor values are the same, and as they make up the numerator in the Q equation the multiplication factor of the Q factor, as the tuning is changed, is the same. Hence there are only a few numbers we need to know.

High osc Q : +13% / -12%
Low osc Q : +17% / -14%

Fall In To Decay

As we know from the Service manual, the target decay times for both oscillators is 60 ms (as we'll see, one of those is totally wrong) and we can now get an idea from that what the decay time variation will be.

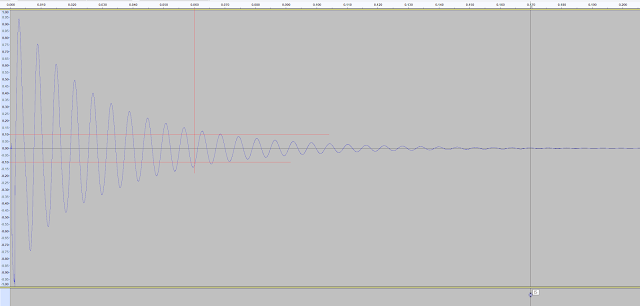
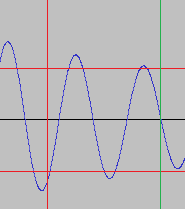
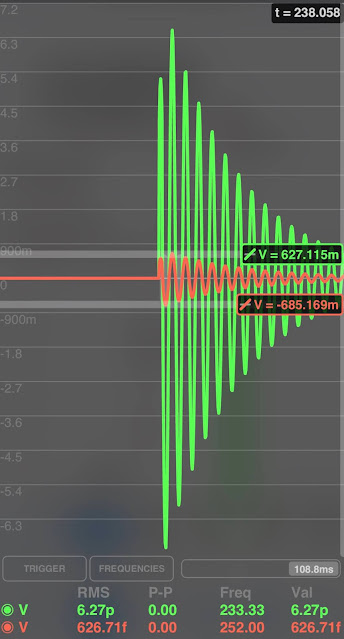
Here is an image from Audacity of a sample of the Low shell of the Roland ACB snare (from my TR-6S)

The vertical red marker shows 60ms and the two horizontal red markers show 1/10 Vpp. As you can see, the amplitude has not decayed to one tenth till later.

Here is a close-up of 60ms.

Now here's a view with 70ms marked.

It's not exact, but the one tenth seems to be around 70ms not 60ms for this low shell.

Now, here's the high shell (note the distortion in this waveform).

Here, I reckon the 1/10 Vpp is reached after about 40ms.

But! Watch out! I recorded this sample without checking the decay setting. The ACB snare has a decay setting, so it's quite easy to get confused. The low shell above was recorded with the setting at the mid-point. I recorded the high shell with the same decay setting and decay time was actually even shorter, at around 30ms. It's harder to tell, due to the distortion.

In simulation I got different results for both of oscillators. In fact it was much closer to the quoted 60ms for the low oscillator at 238 Hz.

This trace has the shell in green and the same oscillator in red, but divided by 10 (a lot easier to do when you only have to type in the value of resistor!). The horizontal markers set a trigger for the trace to stop when they are hit and they are aligned to the the 1/10th signal. The marker at the top indicates that it stopped at 58ms. Not far off!

However, things are very different with the high shell. In another simulated trace you can see it's much shorter.

Here, the trace is triggered at 1/10th again and this timing is much shorter, indicating a decay time of only 11ms! However, we can't forget that the ACB is tuned to 327Hz for the high shell compared to 479Hz for the documented 'typical' value of oscillator with supposed 60ms. Well, I ran the simulation using the revised capacitor setting and tuned to around 479Hz, but it was still only 18ms.

So, the quoted decay time in the Service manual is twice that of the measured time of the ACB recreation on the 808 and a simulated circuit is only half of that? I'm happy for the service manual to be wrong on this - as a typo - but the simulation ought to be a bit more on the money. I have had problems with the simulation being wrong when the bandwidth is set too short (this is iCircuit on my iPhone), but I'm not sure in this case.

So, what about Q?

Q Ball

After failing to understand Q in the last post, I came back determined to get to bottom of this value. Q is started in the Service Manual with an equation for calculating frequency and Q from the values of the capacitors and resistors. This calcluated value is the reference here, but what is Q in terms of time? That's what I want to know.

It's A Factor

I read this article The "Q" factor of an oscillating system by Michael Richmond and the lights went on in my brain at last. No need to derive anything with transfer functions. I just needed to assume one important thing and take it from there.

Let's assume the decay is exponential. In plainer language: a decay of 1/e of the amplitude occurs in the period known as tau (τ). For the ACB Low oscillator this time (as measured) is approximately 28ms, and the freqeuncy is 167Hz.

We can calculate Q from τω0/2, where (angular frequency) ω0 = 2πf.

Hence:

Qlow_acb(measured) = (28ms x 2π x 167Hz) / 2 = 14.96

However, the calculated value for Q - using the equation in the Service Manual - of the revised Low snare is 16.3. Not a million miles away, but not really correct either.

Using the calculated freqeuncy (again from the Service Manual equation) for the revised Low snare and τ measured from a simulation I get:

Qlow_rev(calculated) = (31ms x 2π x 173Hz) / 2 =16.8

Much closer! Considering that the measured τ is perhaps slightly off from the actual point where the decay curve hits 1/e this is pretty good!

Now, let's drop the measurements and only work from the equations and known values of components. I will work back to find the decay time using the calculated Q of 16.3 and freqeuncy of 173Hz, for the revised Low snare design.

Q = 16.3 = τ x (2π x 173Hz / 2)

τ = 16.3 / (2π x 173Hz / 2) = 16.3 / π173 = 30ms.

That is a value for Tau close to the measured 28ms I got for the ACB Low snare at 167Hz. OK. what now?

More generally, still working with a deacy in amplitude of 1/e, I can state that

τ = Q/πf

As Richmond states "after Q/π cycles, [the] amplitude will be (1/e) of its original value".

As one cycle is 1/f

τ = Q/π x 1/f

Or, the time to decay by 1/e is the Q/π times the period of one cycle.

Time For τ

So, as τ is the time for the oscillations to decay by 1/e, I can also work out what the decay time will be when it has reached 0.9! In other words, the time when it is 0.1 or 1/10th the amplitude it started at, as quoted in the 808 Service Manual for 'Decay Time'. This the 60ms I'm trying to tie together. Remember, above I calculated the τ as 30ms for the revised Low snare drum design.

As the curve continues, the amplitude at 2τ will be 1/e of 1/e - which is 1/e^2 or 0.135. This is nearly 1/10th, but not quite.

However, 2 x 30ms is 60ms, so we seem to be nearly back to that 'typical' value from the table in the Service Manual.That's a good indicator, but what is the variable 'a', if aτ equals the decay time?

This is curce an exponential decay graph of the type y= 1/e^x

(when x=0 y =1; x=1 y=1/e^1; x=2 , y=1/e^2 etc.)

I want to know the value of x when y = 0.1

0.1 = 1/e^x

Rearranging, we get

1/0.1 = e^x = 10

If you're a step ahead now you will know that x is calculated as the base e logarithm of 10, or

ln(10) = 2.302585

Shut Up and Calculate!

Phew! Finally, we have a way to calculate the quoted 'decay time' from Q and f. Remember that Q and f can be calculated from the values of the R and C components in the bridged-T network, using the equations Roland provided.

In the example above, where Q = 16.3 and f = 173Hz, and now we know that the decay time is given by:

ln(10)Q/πf = 69ms

OK! I got 67ms in simulation, but I'm pretty happy with this conclusion!

Let's just say that I will be interested to see what decay time I get when I build this thing for real.

Another point is that I could now calculate the Q for the 'typical' low snare shell oscillator in the service manual and any of the other bridged-T oscillators in the then compare to the calculated values from the schematics. The high oscillator is the interesting one though as it doesn't seem at all correct.

Q Bull?

Rearranging again, to derive Q from the quoted decay time from the Typical High snare at 476Hz:

Q x ln(10)/πf = 60ms

and

Q = 60ms / ln(10) / πf = 38.966.

Which is a long way from the calculated Q figures I got for the original and revised high snare circuits (9.9 and 10.7).

Hence is that typical decay time bullshit? Well, not neccesarily. The quoted frequency in that table from the Low snare is 238Hz. So, let's calculate Q for that and see how that looks.

Q = 60ms / ln(10) / πf = 19.483

Which is pretty cose to the values I get for the Low snare, albeit at the lower end of the adjustable range of freqeuncies. I'm not sure what to do with that though. I could find some C and R values that would fit both the Q and f and therefore decay time. That would give a design for a 'typical' low snare as quoted in the table, but there's no real value to that so I'll leave it to the reader as an excercise for a rainy day.

Anyway, back on the actual 808: using the revised circuit value Q of 9.9 and f of ~336Hz the decay time should be:

ln(10) x 9.9/π x 336 = 21.5ms

This is in-line which what I measured for the simulation at 327Hz giving 18ms.

Phew again!

Bouncing Is What Triggers Do Best

A side note on the distortion mentioned above is that the high shell oscillator circuit has a different trigger input to the low. I've been using the low oscillator throughout this to make sure I don't get too thrown off by this.

Conclusions

At last, I can derive values for frequency and decay time of both snare oscillators from the schematic values of the original and revised components in the 808 Service Manual. I can also calculate the frequencies and decay times of the proposed adjustable ranges for both circuits too! What's more, I can also compare these calculated figures to the 'typical' values quoted in the Service Manual and even check other sounds, such as the conga/toms.

Equations

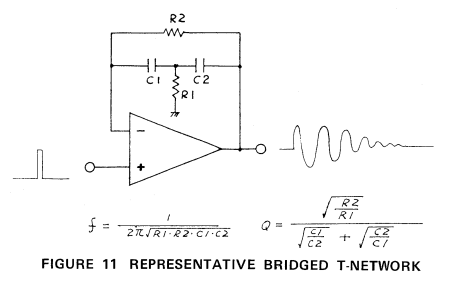
To be clear, these are the equations (note I will use the '.' notation for multiplication)

Frequency of oscillation - f = 1/(2.π.sqrt(R1.R2.C1.C2))

Quality Factor - Q = SQRT(R2/R1)/(SQRT(C1/C2) + SQRT(C2/C1)

Decay Time of oscillation to 1/10 peak - Td = ln(10).Q/π.f

Results

Osc	Revision	R2	R1	C1	C2	**f (Hz)**	Q	Td (ms)
High	Typical					476	~~38.9~~	60
	Original	1000000	2200	6.8E-09	6.8E-09	499.0	10.7	15.7
	Revised	1000000	2200	6.8E-09	1.5E-08	336.0	9.9	21.5
	Original(Hi)	750000	2200	6.8E-09	6.8E-09	576.2	9.2	11.7
		1000000	2200	6.8E-09	6.8E-09	499.0	10.7	15.7
		1250000	2200	6.8E-09	6.8E-09	446.3	11.9	19.6
	Centre(Med)	750000	2200	6.8E-09	1.2E-08	433.7	8.9	15.0
		1000000	2200	6.8E-09	1.2E-08	375.6	10.2	20.0
		1250000	2200	6.8E-09	1.2E-08	336.0	11.5	25.0
	Revised(Low)	750000	2200	6.8E-09	1.5E-08	388.0	8.6	16.2
		1000000	2200	6.8E-09	1.5E-08	336.0	9.9	21.5
		1250000	2200	6.8E-09	1.5E-08	300.5	11.0	26.9
Low	Typical					238.0		60.0
	Original	820000	680	2.7E-08	2.7E-08	249.6	17.4	51.0
	Revised	820000	680	5.6E-08	2.7E-08	173.3	16.3	68.8
	Original(Hi)	570000	680	2.7E-08	2.7E-08	299.4	14.5	35.4
		820000	680	2.7E-08	2.7E-08	249.6	17.4	51.0
		1070000	680	2.7E-08	2.7E-08	218.5	19.8	66.5
	Centre(Med)	570000	680	3.9E-08	2.7E-08	249.1	14.2	41.9
		820000	680	3.9E-08	2.7E-08	207.7	17.1	60.2
		1070000	680	3.9E-08	2.7E-08	181.8	19.5	78.6
	Revised(Low)	570000	680	5.6E-08	2.7E-08	207.9	13.6	47.8
		820000	680	5.6E-08	2.7E-08	173.3	16.3	68.8
		1070000	680	5.6E-08	2.7E-08	151.7	18.6	89.8

Note that the Low Centre(Medium) tuning is 60ms decay time, but the frequency is quite different to the 'typical' value of 238Hz. You can probably see that there are many ways to get the frequency, Q or decay time to match one of the typcal values. Getting all to match the typical figures is another matter...

In conclusion, I have a design for my 8081 Snare Drum. The frequency ranges shown above will give the control I desire and the decay times will not be too far from the normal, even at the extremes.

Appendix

Futile Resistance

In which I confirm that there is no perfect way to tune a bridged-T network with a linear range.

Tuning Dork

As noted above the ideal resistor for R197 is a potentiometer of 820K.

Calculating the oscillation frequency for these values of 197 is not good news though.

i.e. let the range of values be 410K +/- 410K (820K pot):

410K = 353.Hz
820K = 250 Hz
1.23M = 203Hz

Note that the range is uneven with the extremes at +103Hz and - 47Hz, which is uneven.

Get Bent

With a range in mind, what about that unevenness? This not surprising as it's applying a linear change in resistance to a function for the frequency which is 1/f(x), where f(x) involves a square root. As you would expect that will curve the frequency range, it's an inverse power curve, in fact, so even though it's simple to make the mid-point of the control align with 250Hz the rest will not be a straight line.

Plot of frequency of bridged-T network against a linear increase in R2 resistance

https://www.wolframalpha.com/input/?i=plot+1%2F%282*Pi*SQRT%28x*680*0.000000027*0.000000027%29%29+from+x%3D410000+to+1230000

Can the the variable resistor taper be curved to counteract the curve of the 1/f(x) of the frequency range? As we're dealing with resistance and not the voltage output this topic can be misunderstood and some advice on the internets might give the impression that you can convert the taper of a linear variable resistor to curve either way. So what do we want the curve to be?

Required Curve

Firstly let's restate the resistance as: A minimum value is provided by the fixed resistor, the maximum by the variable resistor. Then let's decide what range we require in the frequencies. Staying with the original capacitor values and the lower pitched oscillator ,the middle of the range is 250Hz and around +/-50Hz (or a bit more) is the target, so the limits are 200-300Hz. We know that the resistances for the mid and bottom to achieve that goal and for the value at the top of the range I iterated through a few calculations to get a usable value.

i.e. let the range of frequency be +/- 50Hz):

560K = 302Hz
820K = 250Hz
1.2M = 203Hz

This is a range of 640K for the variable resistor, which is not practically possible to obtain as a potentiometer, even if there curve was ideal. Let's just look at what that resistance taper would have to be in in order to get a straight line through the frequencies though.

Ideal R2 of bridged-T network to obtain linear frequncy range Vs linear R2

Notice that this curve is quite close to ideal. Almost ideal. It's also curved under. If you know what happens when changing the curve by adding resistors in parallel with a pot you will see that this isn't helpful :-)

Taper Reorder

As I mentioned, there are various guides and opinions around the internet with people saying you can adjust the curve of a linear to a log-like (not precise log) or anti-log-like, or indeed vice versa.

Here's how the linear curve changes with a taper resister

https://electronics.stackexchange.com/questions/258443/convert-reverse-log-taper-potentiometer-to-log-audio-taper-potentiometer

However this is misleading. The curve plotted here is not the total resistance across two nodes, but the output voltage (or power or whatever). The resistance across the two nodes, given as e1, is not the the same curve at all. With the wiper at the top the pot the resistance is the combined parallel values and when it's at the bottom the nodes are shorted - zero resistance.

To keep the comparison with the above plots I need a pair of resistor values that will give me a range of 640K, i.e. the parallel resistance is 640K. Using 1M pot with 1.8M taper resistor I plotted the curve.

And as you can see - it curves the wrong way! And there's no way to get it to bend the other way. If Rtaper is increased the curve eventually disappears because the current just cannot get through and it's closing in on open circuit. If Rtaper is smaller the opposite happens and the path of least resistance is through that and there is a eventual flattening of the curve until only the very start gives any increase and then it's stuck at the level of Ttaper. So, that doesn't work!

Falling off a log

I cribbed some actual values from the Alpha datasheet to see what their real log response is like and this is how it compares to the ideal curve and the linear for an imaginary 640K pot.

OK, the Log pot is way off, but can I bring it in line by adding a taper resistor? Curve it back?? Note the factor above for the relationship between the resistors and the curve is given as R2/R1, for the values above that is 1.8. I've plotted that and... It's underwhelming.

Well, okay, it's not good, but what if the value this alpha factor is higher? Errm...Can I achieve that? I will need a value for the R2 which is much higher and still get the range I want of 640K. Hmm! Yes, this is errm and hmm!

Can it be done? Getting a different ratio is easy peasy, but getting that ratio to equate to 640K still is not possible. Damn. If you start with a 1M pot there's one value for the taper resistor which will get you there. 1.8M. We already got that! Well, what if the pot is 500K instead? Well, I hardly have to point out a lower resistance than 640K is not going to get any higher when you put a resistor in parallel. OK. Could I have a dual-log pot 1M, giving me 2M in total? Well, even if you can figure out that wiring, the problem is it's just flipped the maths around and the ratio is now worse. Something like 940K/2M = 0.47. Going the wrong way!

It seems that this trick of flattening out a log taper only works if you make a compromise of the range, but even then the ends of the series are way out. I played around with various values and the curve will bend the right way eventually, but it's nowhere near as close at the basic linear range I got to begin with. It's just not ever going to match up because log and power are not the same curves and there are no precise pots with power curves in the range I want.

Tapering Off

In conclusion the temptation to bend a linear pot just out of alignment doesn't work and trying the same with a log pot is worse. An antilog pot would be the just as bad as the log. So, that's that. I will have to put up with an uneven range.

Norgatronics

SD 80'81 - Tuning Theory